Transformers Explained: Part I

In this post, we'll be going over the high-level architectural overview of transformers. Let's kick off this blog with a simple introduction to transformers

So, what is a transformer?

Transformer is an architecture that uses "attention" to improve the performance of Natural Language Processing(NLP) models. First introduced in the paper Attention Is All You Need, it has become the backbone of several applications in NLP including machine translation, text summarization and language generation. Several extensions such as BERT, GPT and T5 have achieved state-of-the-art results.

Why transformers?

Transformers fixed a few of the salient limitations of RNN-based models that were the standard for NLP tasks

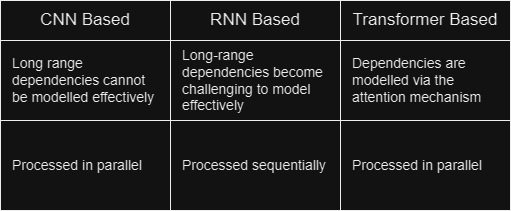
Now that we have the "what" and the "why" out of the way, let us focus on the "how" of the transformer network.

Transformer Architecture Overview

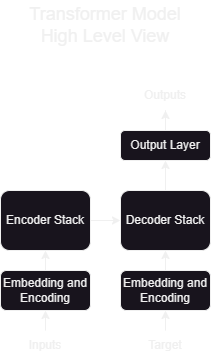
At their very core, most neural transduction models have an encoder-decoder structure.

Encoder: X→Z
Decoder: Z, [y₀...y_i-1]→y_i
where previously generated symbols are used as additional input when generating the next.

In this, the transformer is no different and follows this overall architecture with stacked self-attention and pointwise fully connected layers for both encoder and decoder.

At a slightly more granular level, we can expand the encoder and decoder stacks to reveal the connection between them. We'll be using 6 encoding and decoding layers since that is what the paper prescribes.

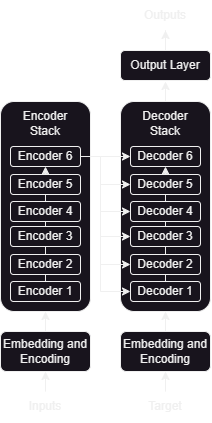
Encoder and Decoder Stacks

Encoder

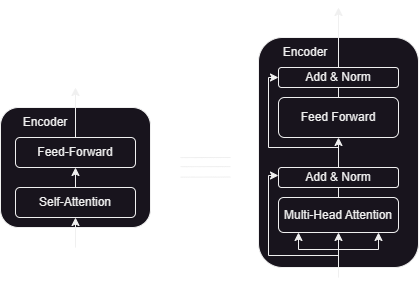
The encoder contains the self-attention layer responsible for computing the relationship between different words in the sequence.
This is followed by a fully connected feed-forward network.
A residual connection wraps around each of the two sub-layers followed by layer normalization. To facilitate this, the outputs of the sublayers are of the same dimension as their inputs and the final equation becomes:
Output_sublayer = LayerNorm(x+Sublayer(x))
where Sublayer(x) is the function implemented by the sub-layer itself

Decoder

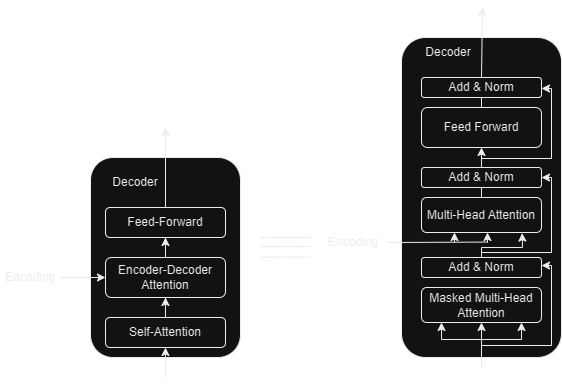
The decoder also implements a self-attention (albeit a masked variant) layer.
This is followed by a encoder-decoder attention layer that takes input from the encoder stack.
Finally just like the encoder, we have a fully connected layer.
The self-attention is masked in order to prevent positions from attending to subsequent positions. This masking combined with the fact that the output embeddings are offset by one position, ensures that the predictions for position i can only depend on the known outputs at positions less than i

Examining the meaning of Attention

At a cursory level, attention enables the model on other words in the input that are closely related to that word.

A more detailed explanation of attention will follow in the upcoming blogs that will cover an explanation for the multi-head aspect of attention as well.

Embeddings and Encodings

Now that we've explored the encoder and decoder at a cursory level, we'll just breeze through the embedding and encoding layer.

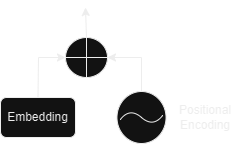
Embeddings
Similar to other sequence transduction models, the transformer network also employs learned embeddings to convert the input tokens and output tokens to vectors of dimension d_model (taken to be 512 in the paper).

Positional Encoding
Since the model allows propagation of tokens in parallel, so far we have not captured any information about the order of the sequence. To fix this, the model uses sine and cosine functions of different frequencies in order to inject some information about the position of the tokens in the sequence.

Great! We have now understood all the components sufficiently to proceed with an understanding of the training and inference of the transformer network.

Model Training

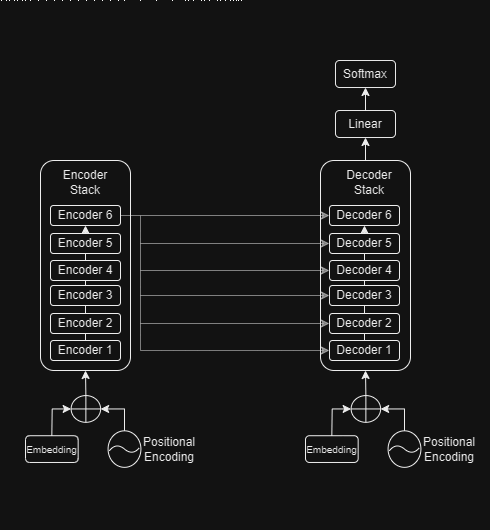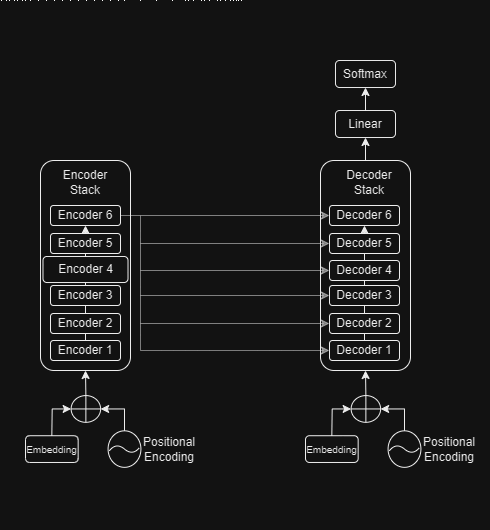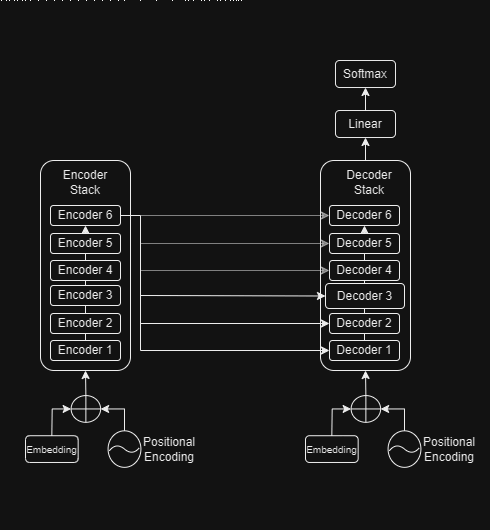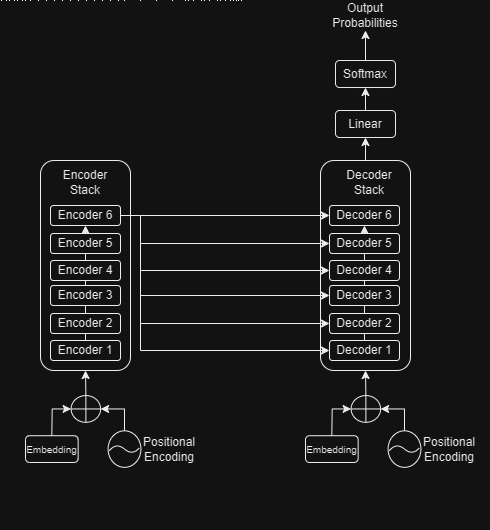
The word probabilities thus generated are used to generate the output sequences. The loss function is used to compare these output sequences with the corresponding target sequences and generate the gradients modify the transformer weights during backpropagation.

Note: Notice how we're using the target sequence to influence model training. This method is known as "teacher forcing". We're essentially giving our model enough hints in order to generate the target sequence with sufficient confidence. This gives it an edge over a "self-learning" approach atleast early on during the model training.

Model Inference

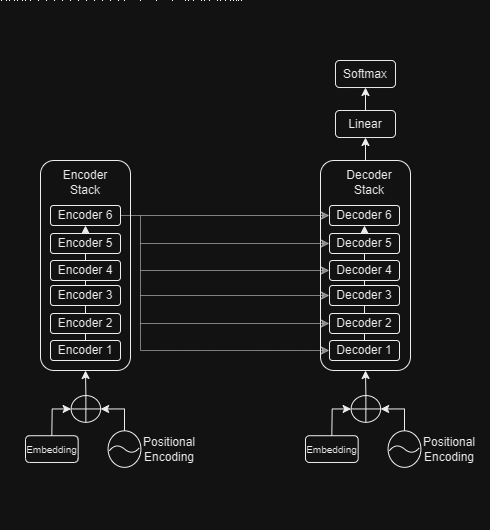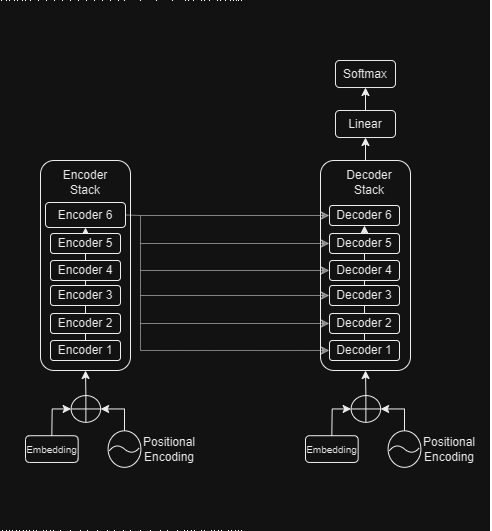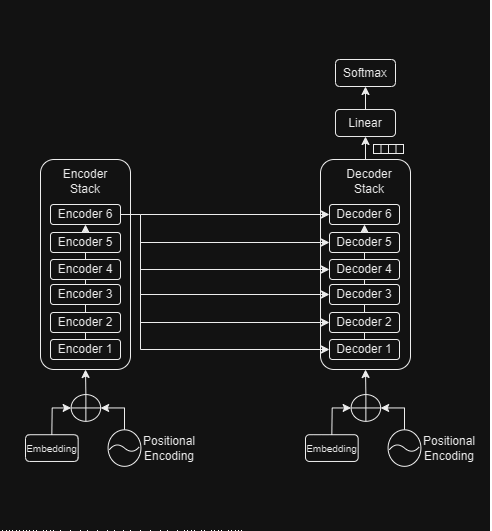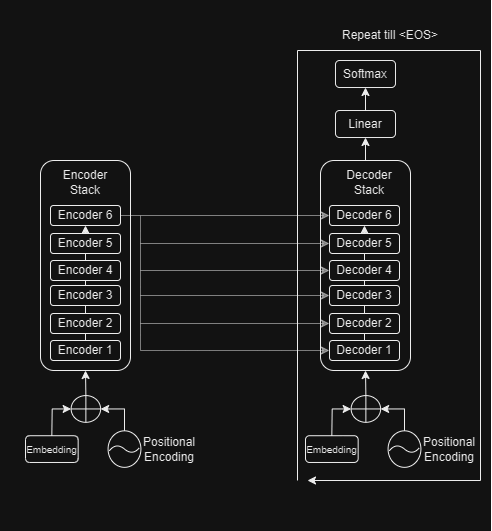
Thus, during inference, we generate the output sequence one token at a time and keep feeding the output sequence so far in a loop till we encounter an end-of-sentence token.

Conclusion

We now have a high-level understanding of the transformer architecture and a basic intuition into why it works so well. In the next blog, we'll focus more deeply into the inner workings of the transformer model.